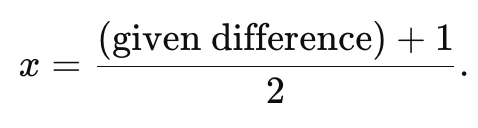Numerical reasoning
Please watch the video above then read the material here
The numerical reasoning section of the JOA is designed to test your mathematical competence.
Numerical reasoning comprises 17 of the 51 questions on the JOA, there are 3 types of question you will encounter, with 3 subcategory of question for worded numerical problems.
3 Missing Value Matrices
The rows, and columns of the matrices both have rules. You must determine what the rule is, up and across the matrix. Across the rule may be multiplication. But down the rule may be subtraction. If you able to determine these rules you will be able to find the answer to the question.
Sequences
You can determine the rule of the sequences by reading the numbers around the missing value. Then continuing the pattern. In previous JOA tests, this used to be a multiple choice question, for the current version of the JOA (2026) its a single entry question.
Worded numerical Problems
Linked Ratio Proportional Problem (Example 1 in video)
The context of these questions will differ, but the format stays the same. Use the unit method. Choose one quantity as 1 unit, then write every other quantity in units relative to it (e.g. A is 6 units, C is one-third of a unit). When you’re given an actual number for any quantity, first divide to find the value of 1 unit, then multiply by the required number of units to get the target. In short: pick a base unit → find 1 unit → scale up to the answer.
Consecutive squares (difference-of-squares) problem. (Example 2 in video)
When a problem says “the square of a number is a fixed amount more than the square of the previous number,” use this shortcut: the gap between consecutive squares is always 2x−1, where x is the unknown number. Set 2x-1 = (the given difference) and solve for X. This equation then becomes
Equal-quotient divisibility problem. (Example 3 in video)
Let the common quotient be q. Then each part = q × its divisor, so
Total = q×(sum of divisors).
For the least total, use q=1 → answer = sum of the divisors.